Note: At the bottom of the post the complete source code
The use of accelerometer and gyroscope to build little robots, such as the self-balancing, requires a math filter in order to merge the signals returned by the sensors.
The gyroscope has a drift and in a few time the values returned are completely wrong. The accelerometer, from the other side, returns a true value when the acceleration is progressive but it suffers much the vibrations, returning values of the angle wrong.
Usually a math filter is used to mix and merge the two values, in order to have a correct value: the Kalman filter . This is the best filter you can use, even from a theoretical point of view, since it is one that minimizes the errors from the true signal value. However it is very difficult (see here) to understand. In fact, the filter needs to be able to calculate the coefficients of the matrices, the process-based error, measurement error, etc. that are not trivial.
In the hobbistic world, recently are emerging other filters, called complementary filters. In fact, they manage both high-pass and low-pass filters simultaneously. The low pass filter filters high frequency signals (such as the accelerometer in the case of vibration) and low pass filters that filter low frequency signals (such as the drift of the gyroscope). By combining these filters, you get a good signal, without the complications of the Kalman filter.
Making a study from a theoretical point of view, the discussion is complicated and is beyond the scope of this tutorial. The complementary filters can be have different ‘orders’. Here I speak about the so-called first-order filter that filter already well, and the second-order filter which filter even better. Clearly, going from first to second order, the algorithm is more complicated to use and perhaps there is no gain so obvious to justify the increase in complexity.
A great introduction to the first order complementary filters applied to the an accelerometer and a gyroscope, comes from MIT (here). It introduces the filter in a a very simple mode. On this document is based the first Arduino algorithm:
// a=tau / (tau + loop time) // newAngle = angle measured with atan2 using the accelerometer // newRate = angle measured using the gyro // looptime = loop time in millis() float tau=0.075; float a=0.0; float Complementary(float newAngle, float newRate,int looptime) { float dtC = float(looptime)/1000.0; a=tau/(tau+dtC); x_angleC= a* (x_angleC + newRate * dtC) + (1-a) * (newAngle); return x_angleC; }
It ‘enough to choose the response time of tau, to send the arguments, ie the angle measured with the accelerometer and the gyroscope, the time of the loop and you get in two lines, the angle calculated by the filter.
The algorithm at the base of the second order complementary filter is described here. Indeed it is not described at all, but now we’ve figured out how the filter works by the MIT’s documentation. The principle is the same, the algorithm is more complicated. The translation of this algorithm for the Arduino:
// newAngle = angle measured with atan2 using the accelerometer // newRate = angle measured using the gyro // looptime = loop time in millis() float Complementary2(float newAngle, float newRate,int looptime) { float k=10; float dtc2=float(looptime)/1000.0; x1 = (newAngle - x_angle2C)*k*k; y1 = dtc2*x1 + y1; x2 = y1 + (newAngle - x_angle2C)*2*k + newRate; x_angle2C = dtc2*x2 + x_angle2C; return x_angle2C; }
Here too we just have to set the k and magically we get the angle.
If we want to apply the Kalman filter, we can re-use one of the codes already present in internet. This is the code that I copied from the Arduino forum (here):
// KasBot V1 - Kalman filter module float Q_angle = 0.01; //0.001 float Q_gyro = 0.0003; //0.003 float R_angle = 0.01; //0.03 float x_bias = 0; float P_00 = 0, P_01 = 0, P_10 = 0, P_11 = 0; float y, S; float K_0, K_1; // newAngle = angle measured with atan2 using the accelerometer // newRate = angle measured using the gyro // looptime = loop time in millis() float kalmanCalculate(float newAngle, float newRate,int looptime) { float dt = float(looptime)/1000; x_angle += dt * (newRate - x_bias); P_00 += - dt * (P_10 + P_01) + Q_angle * dt; P_01 += - dt * P_11; P_10 += - dt * P_11; P_11 += + Q_gyro * dt; y = newAngle - x_angle; S = P_00 + R_angle; K_0 = P_00 / S; K_1 = P_10 / S; x_angle += K_0 * y; x_bias += K_1 * y; P_00 -= K_0 * P_00; P_01 -= K_0 * P_01; P_10 -= K_1 * P_00; P_11 -= K_1 * P_01; return x_angle; }
To get the answer, you have to set 3 parameters: Q_angle, R_angle,R_gyro. The activity is a bit complicated .
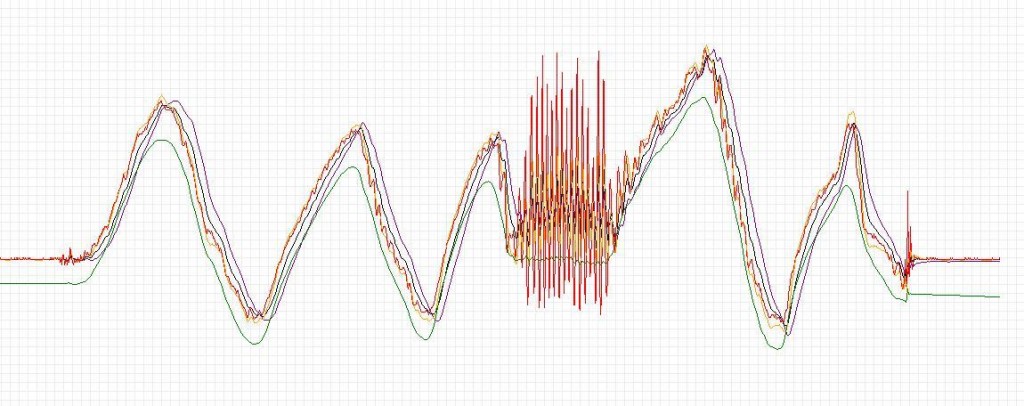
But what happens with these algorithms? Similar curves are obtained? Here’s a comparison:
There are 5 curves:
Color lines:
- Red – accelerometer
- Green – Gyro
- Blue – Kalman filter
- Black – complementary filter
- Yellow – the second order complementary filter
As you can see the signals filtered are very similarly. Note that in the presence of vibrations, the accelerometer (red) generally go crazy. The gyro (green) has a very strong drift increasing int the time.
Now let’s see a comparison only between a filtered signal. That kalman (green), complementary (black) and complementary second-order (yellow). You can see how the Kalman is a bit late vs complementary filters, but it is more responsive to the vibration. In this case the second order filter does not return an ideal curve, probably I have to work a bit on the coefficients.
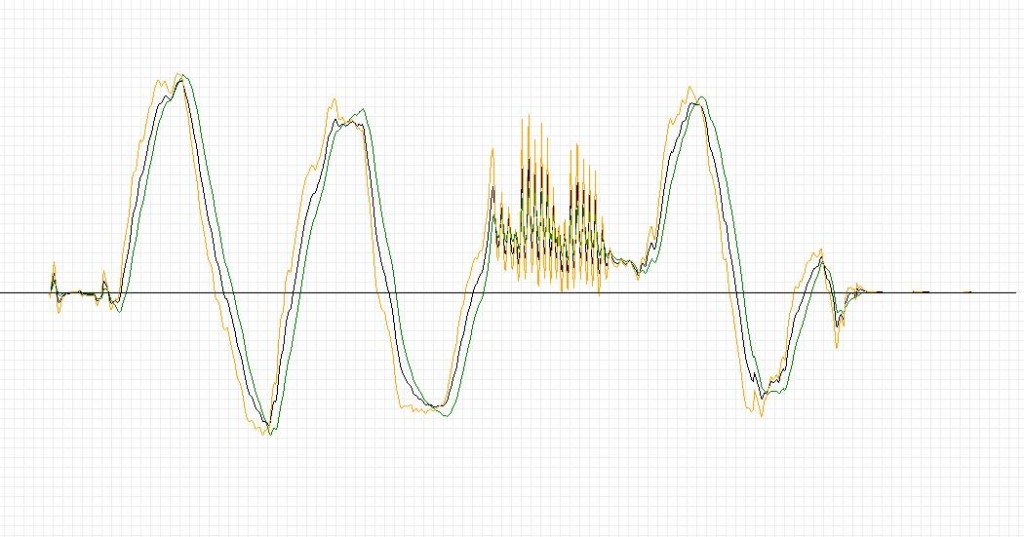
In conclusion I think that the complementary filter, in this case the first order, can be used in place of the Kalman filter. The smoothing is good and the algorithm is much simpler than Kalman.
The hardware I used was composed of:
– Arduino 2009
– 6-axis IMU SparkFun Razor 6 DOF